Learning From Scratch by Thinking Fast and Slow with Deep Learning and Tree Search

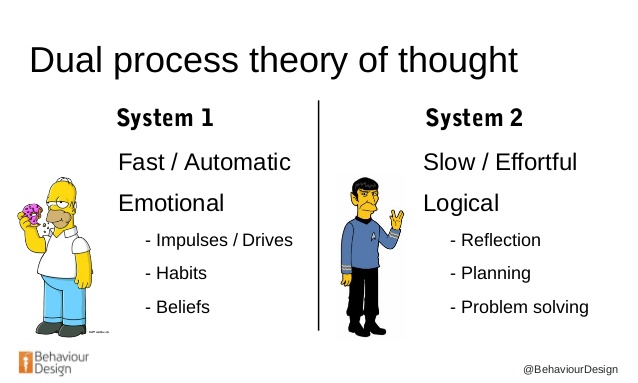
According to dual process theory human reasoning consists of two different kinds of thinking. System 1 is a fast, unconscious and automatic mode of thought, also known as intuition. System 2 is a slow, conscious, explicit and rule-based mode of reasoning that is believed to be an evolutionarily recent process.

image credit

When learning to complete a challenging planning task, such as playing a board game, humans exploit both processes: strong intuitions allow for more effective analytic reasoning by rapidly selecting interesting lines of play for consideration. Repeated deep study gradually improves intuitions. Stronger intuitions feedback to stronger analysis, creating a closed learning loop. In other words, humans learn by thinking fast and slow¹.

What’s wrong with current Deep RL?

In current Deep Reinforcement Learning (RL) algorithms such as Policy Gradients² and DQN³, neural networks make action selections with no lookahead; this is analogous to System 1. Unlike human intuition, their training does not benefit from a ‘System 2’ to suggest strong policies.

A criticism of some AI algorithms such as AlphaGo⁴ is that they use a database of human expert play⁴. In the initial phase of training the RL agent mimics the moves of a human expert – only after this initial phase does it begin to learn potentially more powerful super-human play. This is somewhat unsatisfactory since the resulting algorithm may be heavily biased toward a human style of playing, blind to potentially more powerful lines of play. Whilst, in areas such as game playing, it may be natural to assume that there will be a database of human expert play available, in other settings in which we wish to train an AI machine, no such database may be available. Therefore, showing how to train a state-of-the-art board game player ex nihilo is a major challenge for AI.

Expert Iteration (ExIt)

Expert Iteration⁵ (ExIt) is a general framework for learning that we introduced in May 2017 and can result in powerful AI machines, without needing to mimic human strategies.

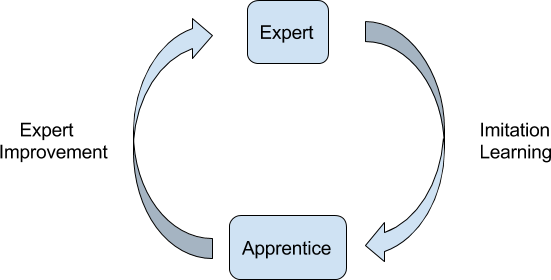
ExIt can be viewed as an extension of Imitation Learning (IL) methods to domains where the best known experts are unable to achieve satisfactory performance. In standard IL an apprentice is trained to imitate the behaviour of an expert. In ExIt, we extend this to an iterative learning process. Between each iteration, we perform an Expert Improvement step, where we bootstrap the (fast) apprentice policy to increase the performance of the (comparatively slow) expert.

To give some intuition around this idea, consider playing a board game such as chess. Here the expert is analogous to chess player playing on slow time controls (having lots of time to decide on her move), and the apprentice is playing on blitz time controls (having little time to decide which move to make).

During independent study, the player considers multiple possible moves from a position, thinking deeply (and slowly) about each possible move. She discovers which moves are successful and which are not in this position. When she encounters a similar board state in the future, her study will have given her an intuitive understanding of what moves are likely to be good, allowing her to play well, even under blitz time controls. Her intuition is imitating the strong play she calculated via deep thinking. Humans do not become become excellent chess players by only playing blitz matches, deeper study is an essential part of the learning process.

For an AI game playing machine, this imitation could be achieved, for example, by fitting a neural network to the move made by another `machine expert’ from a game position. The apprentice learns a fast policy that is able to quickly imitate the play of the expert on the moves seen so far. A key point here is that, assuming that there is structure underlying the game, Machine Learning enables the apprentice to generalise their intuition to take quick decisions on positions not previously seen. That is, the apprentice isn’t just a creating a look-up-table of moves made by the human from a fixed database of positions. The neural network thus plays the role of both generalising and imitating the play of the expert.

Now that the apprentice has learned a fast imitation of the expert (on the moves seen so far), it can try to be of use to the expert. When the expert now wishes to make a move, a small set of candidate moves are suggested very quickly by the apprentice which the expert can then consider in depth, possibly also guided during this slow thought process by other quick insights from the apprentice.

At the end of this phase, the expert will have made a set of apprentice-aided moves, with each move being typically much stronger than either the apprentice or expert could have made alone.

The above process now repeats, with the apprentice retraining on the moves suggested by the expert. This completes one full iteration of the learning phase and we iterate this process until the apprentice converges.

From a Dual Process perspective, the Imitation Learning step is analogous to a human improving their intuition for the task by studying example problems, while the Expert Improvement step is analogous to a human using their improved intuition to guide future analysis.

Tree Search and Deep Learning

Exit is a general strategy for learning and the apprentice and expert can be specified in a variety of ways. In board games Monte Carlo Tree Search (MCTS) is a strong playing strategy⁶ and is a natural candidate to play the role of the expert. Deep Learning has been shown to be a successful method to imitate the play of strong players⁴ which we therefore use as the apprentice.

At the Expert Improvement phase we use the apprentice to direct the MCTS algorithm toward promising moves, effectively reducing the game tree search breadth and depth. In this way, we bootstrap the knowledge acquired by Imitation Learning back into the planning algorithm.

The board game Hex

Hex is a classic two-player board game played on a $n\times n$ hexagonal grid. The players, denoted by colours black and white, alternate placing stones of their colour in empty cells. The black player wins if there is a sequence of adjacent black stones connecting the North edge of the board to the South edge. White wins if he achieves a sequence of adjacent white stones running from the West edge to the East edge.

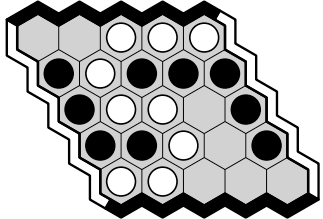An example game on a $5\times 5$ Hex board.

The above represents play on a $5\times 5$ board, with white winning (reproduced from ⁷). Hex has deep strategy, making it challenging for machines to play and its large action set and connection-based rules means it shares similar challenges for AI to Go. Compared to Go, however, the rules are simpler and there can be no draws.

Because the rules of Hex are so simple, the game is relatively amenable to mathematical analysis (compared for example to Go) and the current best machine player MoHex⁷ uses a combination of MCTS and smart mathematical insights. MoHex has won every Computer Games Olympiad Hex tournament since 2009. It is noteworthy, that MoHex uses a rollout policy trained on datasets of human expert play.

We wanted to see if we can use our ExIt training strategy to learn an AI player than can outperform MoHex, without using any game-specific knowledge or human example play (beside the rules of the game). To do this, our expert is a MCTS player that is guided by the apprentice neural network. Our neural network is a form of deep convolutional network with two output policies – ones for black play and one for white (see ⁵ for details).

Expert Improvement is achieved by using the modified MCTS formula⁸

$$UCT(s,a) + w \frac{\hat{\pi}(a|s)}{n(s,a)+1} \tag{1}\label{eq:uct}$$

Here $s$ is the state of the Hex board, $a$ is a possible action (i.e. move) from $s$. The term $UCT(s,a)$ represents the classical Upper Confidence Bound for Trees⁶ used in MCTS. The additional term helps the neural network apprentice guide the search to more promising moves. In this term $\hat{\pi}$ is the policy (suggested relative strength of each possible action $a$ from the board state $s$) of the apprentice and $n(s,a)$ the number of visits currently made by the search algorithm through state $s$ and taking action $a$; $w$ is an empirically chosen weighting factor that balances the slow thinking of the expert with the fast intuition of the apprentice. Through the additional term, the neural network apprentice guides the search to more promising moves, and rejects weak moves more quickly.

To generate the data for training the apprentice (during each Imitation Learning phase), the batch approach generates data afresh, discarding all data from previous iterations. We also consider a online version in which we instead keep a running buffer of the most recent moves generated; we further consider an online version that retains all data, but with exponentially more data from more recent experts (which correspond to the strongest play). A comparison of these different approaches is given below in which we compare the strength (measured in terms of the ELO score) of each learned policy network against a measure of training time.

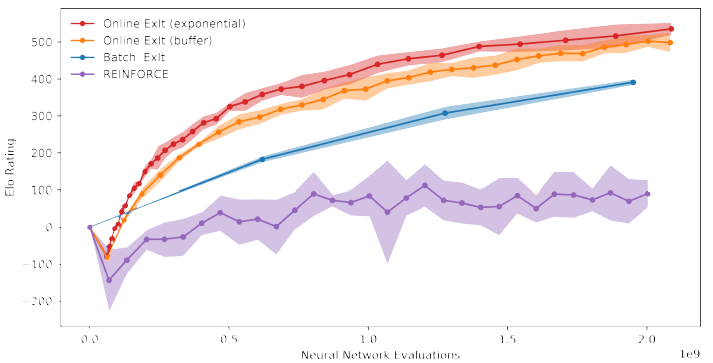
We also show the result of using a more traditional Reinforcement Learning approach in which a policy $\hat{\pi}(a\vert s)$ is learned only through self play (i.e. no MCTS). This is essentially the method used within AlphaGo⁴ to train their policy network. The figure shows that the ExIt training approach is considerably more effective than more classical approaches. It is worth noting that in this example training has not yet fully converged and the apprentice would be expected to improve in ability further given additional training time.

In our paper⁵ we include an additional mechanism to improve play, namely a value network $V^{\hat{\pi}}(s)$ that approximates the probability that the apprentice (alone) would win the game from position $s$. Both the policy and value network are then used in combination to help guide the final apprentice-aided MCTS player. The policy network and value networks guide the final MCTS player using an equation similar to \eqref{eq:uct}, but modified to include the apprentice’s value of the state $s$ (see ⁵ for details).

Our final MCTS player outperforms the best known machine Hex player, MoHex, beating it in 75% of games played on a $9\times 9$ board. These results are even more remarkable considering that training has not fully converged. A couple of examples of game-play of our ExIt trained player versus the state-of-the-art MoHex player are shown below⁹. We contrast the play of each algorithm when started at the same position. See the paper⁵ for more examples.

ExIt (black) versus MoHex (white)

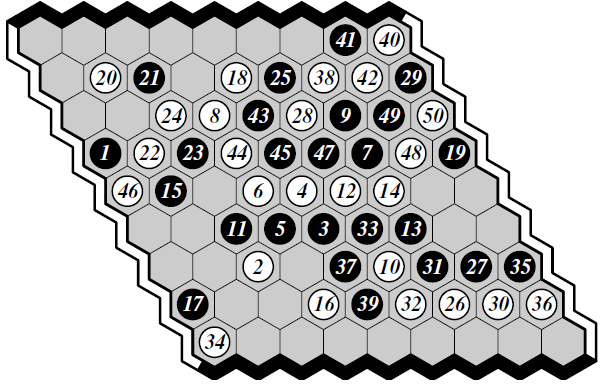MoHex (black) versus ExIt (white)

Why does ExIt work so well?

Imitation Learning is generally appreciated to be easier than Reinforcement Learning, and this partly explains why ExIt is more successful than model-free methods like REINFORCE.

Furthermore, for MCTS to recommend a move, it must be unable to find any weakness with its search. Effectively, therefore, a move played by MCTS is good against a large selection of possible opponents. In contrast, in regular self play (in which the opponent move is made by the network playing as the opposite colour), moves are recommended if they beat only this single opponent under consideration. This is, we believe, a key insight into why ExIt works well (when using MCTS as the expert) — the apprentice effectively learns to play well against many opponents.

Relation to AlphaGo Zero

AlphaGo Zero¹⁰ (developed independently of our work¹¹) also implements an ExIt style algorithm and shows that it is possible to achieve state-of-the-art performance in Go without the use of human expert play. A detailed comparison of the approaches is given in our paper⁵.

Summary

Expert Iteration is a new Reinforcement Learning algorithm, motivated by the dual process theory of human thought. ExIt decomposes the Reinforcement Learning into the separate subproblems of generalisation and planning. Planning is performed on a case-by-case basis, and only once a strong plan is found is the resultant policy generalised. This allows for long-term planning and results in faster learning and state-of-the-art final performance, particularly for challenging problems. This training strategy is powerful enough to learn state-of-the-art board game AI players without requiring any examples of expert human play.

References

1. D. Kahneman. Thinking, Fast and Slow. Macmillan, 2011. ↩

2. R. J. Williams. Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning. Machine Learning, 8(3-4):229–256, 1992. ↩

3. V. Mnih et al. Human-Level Control through Deep Reinforcement Learning. Nature, 518(7540):529–533, 2015. ↩

4. D. Silver et al. Mastering the Game of Go with Deep Neural Networks and Tree Search. Nature, 529(7587):484–489, 2016. ↩ ↩² ↩³ ↩⁴

5. T. Anthony, Z. Tian and D. Barber. Thinking Fast and Slow with Deep Learning and Tree Search, Neural Information Processing Systems (NIPS 2017). In Press. ↩ ↩² ↩³ ↩⁴ ↩⁵ ↩⁶

6. L. Kocsis and C. Szepesvári. Bandit Based Monte-Carlo Planning. In European Conference on Machine Learning, pages 282–293. Springer, 2006. ↩ ↩²

7. S.-C. Huang, B. Arneson, R. Hayward, M. Müller, and J. Pawlewicz. MoHex 2.0: A Pattern-Based MCTS Hex Player. In International Conference on Computers and Games, pages 60–71. Springer, 2013. ↩ ↩²

8. S. Gelly and D. Silver. Combining Online and Offline Knowledge in UCT. In Proceedings of the 24th International Conference on Machine learning, pages 273–280. ACM, 2007. ↩

9. Thanks to Ryan Hayward for providing a tool to draw Hex positions. ↩

10. D. Silver, et al. Mastering the game of Go without human knowledge. Nature 550:354–359, October 2017. ↩

11. T. Anthony, Z. Tian and D. Barber. Thinking Fast and Slow with Deep Learning and Tree Search. arXiv CoRR:abs/1705.08439, May 2017. ↩